Network Theorems and Their Applications

Network theorems are mathematical tools and principles that allow us to simplify and analyze electrical circuits more efficiently. Instead of solving circuits with multiple equations, these theorems offer quicker methods to find voltages, currents, and power.

USERONE March 18, 2025

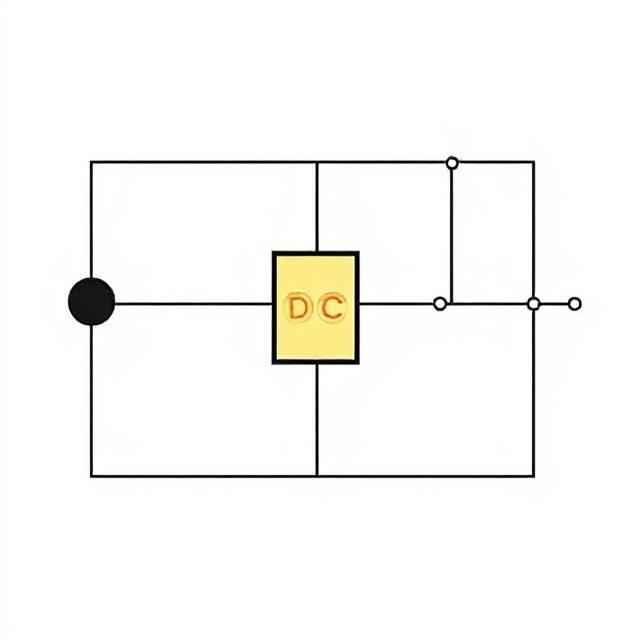
Analyzing electrical circuits can sometimes be complex, especially when they involve many components. Fortunately, Network Theorems provide shortcuts and powerful techniques to simplify circuit analysis. These theorems are useful for both DC and AC circuits and are foundational in electrical and electronics engineering.

What Are Network Theorems?

Key Network Theorems

1. Ohm’s Law (Foundation)

Before diving into the theorems, remember:

$V = I R$ V = IR

This is the basic law for understanding circuit behavior.

2. Superposition Theorem

In a linear circuit with more than one independent source, the total response (current or voltage) in any element is the sum of the responses caused by each source acting alone, with all other independent sources turned off.

Application:

Turn off all sources except one (replace voltage sources with short circuits and current sources with open circuits).
Analyze circuit.
Repeat for other sources and sum results.

3. Thevenin’s Theorem

Any linear two-terminal circuit can be replaced by a single voltage source (Vth) in series with a resistor (Rth).

Steps:

Remove the load resistor.
Find open-circuit voltage (Vth).
Find equivalent resistance (Rth) with sources turned off.
Replace original network with Thevenin equivalent.

Application:
Simplifies complex parts of a circuit, especially useful for analyzing load behavior.

4. Norton’s Theorem

Similar to Thevenin’s, but uses a current source (In) in parallel with a resistor (Rn).

Steps:

Find short-circuit current (In) across load terminals.
Find equivalent resistance (same as Rth).
Replace original network with Norton equivalent.

Tip:
You can convert between Thevenin and Norton forms:

$V_{t h} = I_{n} \times R_{n}$ V_{th} = I_n \times R_n

5. Maximum Power Transfer Theorem

Maximum power is transferred from the source to the load when the load resistance (RL) is equal to the Thevenin resistance (Rth) of the network supplying power.

Application:
Useful in designing communication systems and amplifiers for best performance.

6. Millman’s Theorem

Used to simplify multiple parallel voltage sources with series resistances into a single equivalent voltage source.

Formula:

$V_{e q} = \frac{\sum (\frac{V_{i}}{R_{i}})}{\sum (\frac{1}{R_{i}})}$ V_{eq} = \frac{\sum \left( \frac{V_i}{R_i} \right)}{\sum \left( \frac{1}{R_i} \right)}

Application:
Reduces parallel networks to one source quickly.

7. Reciprocity Theorem (for linear, bilateral networks)

If a voltage source in one branch causes a current in another, then placing the same source in the second branch will cause the same current in the first.

Limitation:
Only valid for single-source AC or DC linear networks.

When and Why to Use These Theorems

Theorem	Best Used For
Superposition	Multiple sources
Thevenin/Norton	Analyzing load effect or simplifying a sub-network
Maximum Power	Optimizing power delivery
Millman	Combining voltage sources in parallel
Reciprocity	Signal paths in communication networks

Real-Life Applications

Designing and analyzing amplifiers.
Simplifying power systems.
Telecommunications networks.
Troubleshooting complex electrical circuits.
Electronic load testing and optimization.

Summary

Network theorems are essential tools in electrical engineering that make complex circuit analysis easier and faster. They help in breaking down circuits into simpler parts using methods like Superposition, Thevenin’s and Norton’s Theorems, and others. These theorems are widely used in both theoretical studies and practical applications, such as power systems, electronics, and communication circuits. Learning to apply these effectively will save time and make circuit analysis much more manageable.