How Interest Works Simple vs. Compound Interest in INR

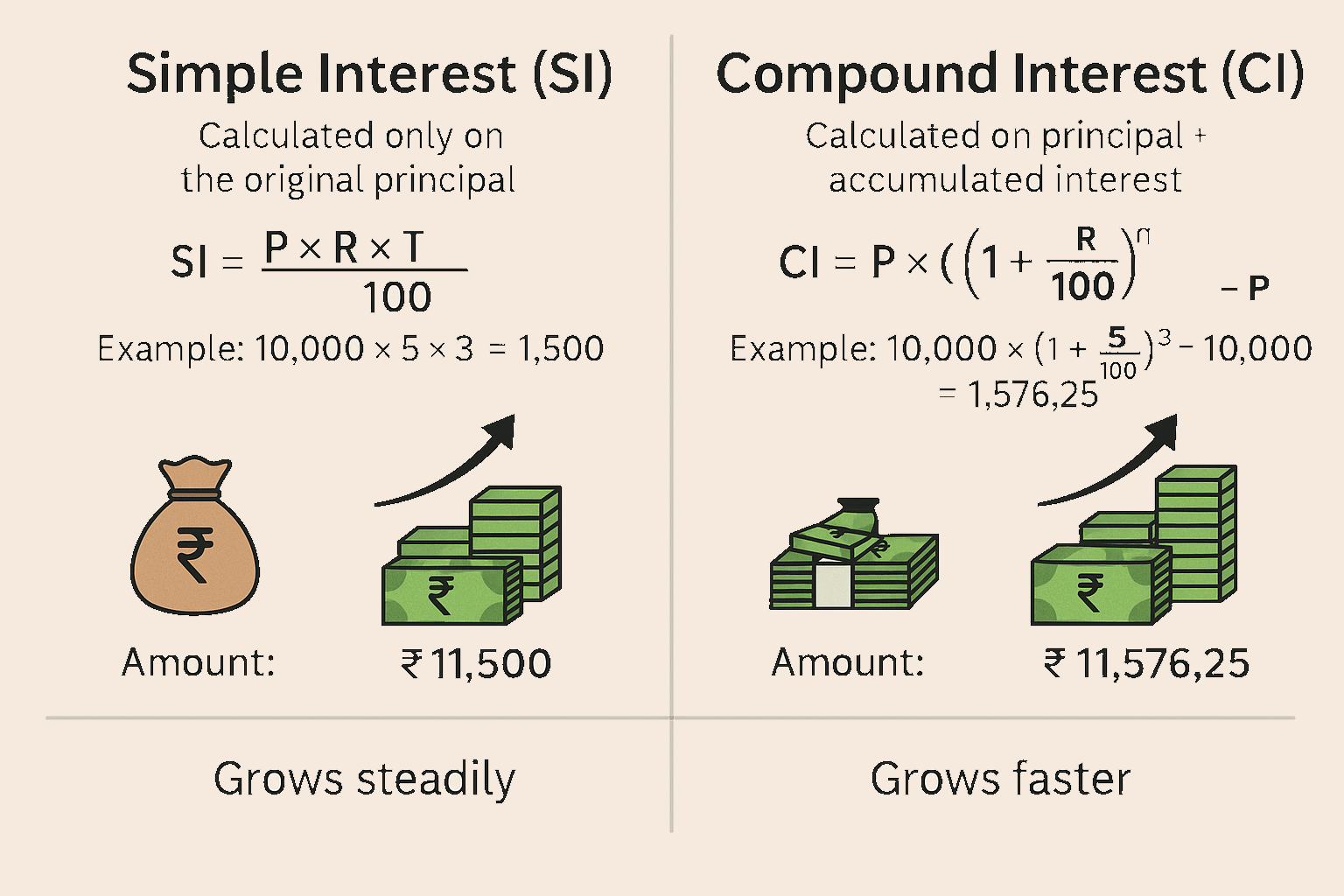
Simple Interest (SI) and Compound Interest (CI) in the context of Indian Rupees (INR) with easy-to-understand examples.

1. Simple Interest (SI) in INR

Simple Interest is the interest that is calculated only on the principal amount (the original amount you invested or borrowed) for the entire time period. It doesn’t get added to the principal over time.

Formula :

$$text{SI} = P times frac{R}{100} times T$$

Where:

• P = Principal amount (the initial money invested or borrowed in INR)
• R = Rate of interest per year (in percentage)
• T = Time period in years

How Simple Interest works:

• Interest is calculated only on the original principal.
• The amount of interest you pay (or earn) remains the same every year.

Example:

Let’s say you borrow ₹10,000 for 3 years at an interest rate of 5% per year.

• P = ₹10,000
• R = 5% (or 0.05 as a decimal)
• T = 3 years

Now, calculate the interest:

$$text{SI} = 10,000 times frac{5}{100} times 3 = 10,000 times 0.05 times 3 = ₹1,500$$

So, after 3 years, you will pay ₹1,500 as interest. The total amount to be repaid after 3 years will be:

$$text{Total Amount} = text{Principal} + text{Interest} = ₹10,000 + ₹1,500 = ₹11,500$$

Thus, you would owe ₹11,500 after 3 years.

2. Compound Interest (CI) in INR

Compound Interest is more interesting because the interest is calculated on both the principal and the interest that has accumulated over time. In simple words, it’s “interest on interest.”

Formula:

$$text{CI} = P times left( 1 + frac{R}{100n} right)^{n times T} – P$$

Where:

• P = Principal amount (the initial money invested or borrowed in INR)
• R = Rate of interest per year (in percentage)
• T = Time period (in years)
• n = Number of times interest is compounded per year (e.g., annually, quarterly, monthly)

How Compound Interest works:

• Interest is added to the principal at regular intervals, so it grows faster.
• The more frequently the interest is compounded (monthly, quarterly), the more you will earn or owe.

Example:

Let’s say you invest ₹10,000 for 3 years at an interest rate of 5% per year, but this time, the interest is compounded annually (once a year).

• P = ₹10,000
• R = 5% (or 0.05 as a decimal)
• T = 3 years
• n = 1 (since it’s compounded annually)

Now, calculate the total amount after 3 years:

$$text{Total Amount} = 10,000 times left( 1 + frac{5}{100 times 1} right)^{1 times 3} = 10,000 times (1.05)^3 = 10,000 times 1.157625 = ₹11,576.25$$

So, after 3 years, the total amount you will have is ₹11,576.25. The interest earned is:

$$text{CI} = 11,576.25 – 10,000 = ₹1,576.25$$

This shows that compound interest gives you ₹1,576.25 in interest after 3 years, which is more than the ₹1,500 from simple interest.

3. Key Differences Between Simple and Compound Interest

4. Types of Interest

• Annual Interest: Interest is calculated and added once per year.
• Quarterly Interest: Interest is calculated and added every 3 months.
• Monthly Interest: Interest is calculated and added every month.
• Continuous Compound Interest: Interest is compounded continuously over time. This is used for more advanced calculations and involves exponential growth.

Summary

• Simple Interest is easier to calculate and remains constant over time.
• Compound Interest grows faster because interest is added to the principal at regular intervals, meaning you earn (or owe) more over time.
• Compound Interest is more beneficial when the interest is compounded more frequently (like monthly or quarterly) and over long periods.

To Recap with an Example:

• Simple Interest for ₹10,000 at 5% per year for 3 years = ₹1,500 (Total: ₹11,500)
• Compound Interest for ₹10,000 at 5% per year for 3 years (compounded annually) = ₹1,576.25 (Total: ₹11,576.25)